Equazione del moto in oceanografiaPrerequisiti: Non lasciamoci spaventare dalle equazioni del moto, perché la loro chiave di lettura consiste nell'applicare la semplicissima II Legge del moto di Newton:F = m * a | Forza risultante uguale massa per accelerazione | [1] |
Il primo passo per giungere all'equazione del moto consiste nel trattare la [1] in modo da mettere in risalto l'accelerazione:Ricordando che l'accelerazione è esprimibile in termini differenziali come derivata della velocità vettoriale rispetto al tempo, possiamo sostituire al simbolo a l'espressione (ricordando che si specifica che una grandezza è vettoriale aggiungendo una freccia sopra al simbolo che esprime la grandezza):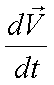
Passiamo ora a considerare le diverse forze agenti sull'unità di massa (considerando una massa unitaria, cioè m = 1, possiamo eliminare dalla [2] il termine relativo alla massa, cosicché la [2] diventa a = F), in quanto nella [1] F può esprimere la risultante di più forze.Le forze che agiscono sull'unità di massa sono:La forza di gradienteLa forza (apparente) di Coriolis (dal nome del fisico francese Coriolis, è una forza fittizia alla quale sembra soggetto un corpo che si muove entro un sistema in rotazione. Questa forza apparente è legata all'accelerazione dell'oggetto provocata dalla rotazione).La forza di gravitàLe forze di attrito e di marea
Diamo ora un primo sguardo all'equazione del moto, scritta in forma differenziale, a cui giungeremo al termine del nostro cammino: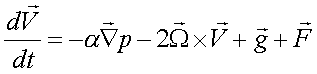
ricordando che essa esprime soltanto in maniera più articolata la semplice relazione a = F. Infatti, nel primo membro troviamo l'accelerazione espressa sotto forma di derivata, mentre nel 2° membro troviamo la somma di tutte le forze che agiscono sull'unità di massa.Per il momento, accontentiamoci di riconoscere tutti i termini che fanno parte dell'equazione: Partiamo dal termine relativo alla pressione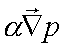 , per vedere come viene ricavato. , per vedere come viene ricavato. Immaginiamo un volumetto rettangolare, immerso in un fluido, avente come lati dx, dy e dz (il simbolo d sta ad indicare una piccola variazione finita). Immaginiamo un volumetto rettangolare, immerso in un fluido, avente come lati dx, dy e dz (il simbolo d sta ad indicare una piccola variazione finita).
La forza agente nella direzione della x su questo volumetto dovuta alla pressione idrostatica sarà:+ pdydzsulla faccia di sinistra, e - (p+dp) dydzsulla faccia destra (il segno meno sta a significare che la forza su questa faccia agisce nella direzione negativa dell'asse x). |  La faccia inferiore dxdy: La faccia inferiore dxdy:
|  La faccia anteriore dxdz: La faccia anteriore dxdz:
| 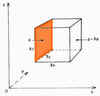 La faccia dydz di sinistra: La faccia dydz di sinistra:
| La forza di pressione netta agente nella direzione x sarà dunque la somma di queste due | + pdydz - (p+dp) dydz == + pdydz - pdydz - dpdydz == - dpdydz. | Se consideriamo il vettore unitario i nella direzione delle x, possiamo riscrivere | - dpdydz | come | 
| oppure, introducendo le derivate parziali, come: | 
| La forza per unità di volume è (dxdydz =1): | 
| e la forza per unità di massa è (ricordare che r = m/V, per cui V = m/r. Se m = 1 allora V = 1/r): | 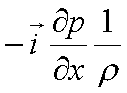
| ricordando che a (volume specifico) è l'inverso della densità, possiamo riscrivere l'ultima espressione così: | 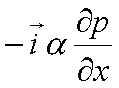
| Se ripetiamo lo stesso ragionamento per tutte le direzioni (considerando per l'asse y il vettore unitario j, e per l'asse z il vettore unitario k) seguendo le stesse operazioni impiegate per la direzione x, la forza totale di pressione per unità di massa sarà: | 
| che, introducendo il simbolo del cosiddetto operatore gradiente  : : | 
| può essere riscritta in forma più abbreviata: | 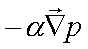
|
Per vedere lo sviluppo del prodotto vettoriale relativo all'accelerazione di Coriolis, clicca qui.L'equazione: 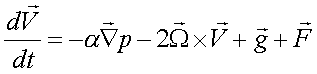 poiché la velocità è espressa in termini vettoriali, può essere riscritta sotto forma delle tre equazioni componenti secondo le coordinate x, y e z e le loro rispettive componenti u, v e w che sono rispettivamente positive nelle direzioni est, nord e verso l'alto, con l'origine delle coordinate posta al livello della superficie marina:(secondo l'asse x) | 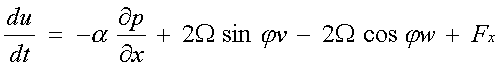 | (secondo l'asse y) | 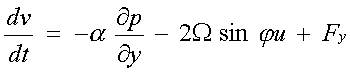 | (secondo l'asse z) | 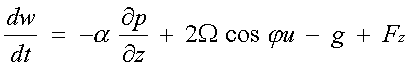 |
Note:Il fattore 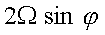 viene spesso indicato con la lettera f (parametro di Coriolis), cosicché, ad esempio: viene spesso indicato con la lettera f (parametro di Coriolis), cosicché, ad esempio:
|
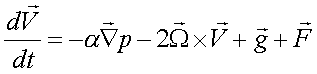
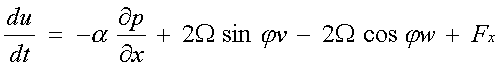
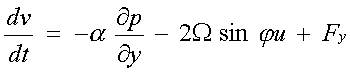
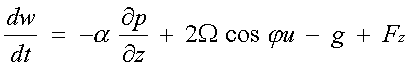
![]()