Matrici e determinanti
Cosa impareremo:
|
Matrice, elementi della matrice, riga, colonna, matrice quadrata,
ordine della matrice, determinanti delle matrici del primo e del secondo
ordine, determinante, complementi algebrici, determinanti
di matrici di ordine superiore al secondo, regola di Sarrus,.
|
Dati m * n numeri si chiama matrice la tabella:
|
 |
Gli m * n numeri, detti ELEMENTI della matrice,
sono contrassegnati da due indici il primo dei quali indica la RIGA di
appartenenza e il secondo la COLONNA di appartenenza.
|
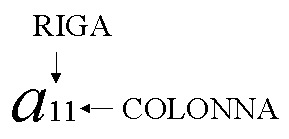 |
Se m = n la matrice è detta QUADRATA e di ORDINE n.
|
|
Si chiama complemento algebrico dell'elemento di matrice (quadrata) ah,k
, e si indica con Ah,k , il determinante della matrice ottenuta
sopprimendo la riga h e la colonna k della matrice di partenza, preceduto
dal segno + o dal segno - a seconda che il numero h + k è pari o
dispari.
|
Esempio.
Data la matrice del terzo ordine:
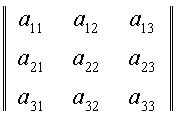
Il complemento algebrico di a22 è:

Il complemento algebrico di a21 è:

|
Il determinante di una matrice (quadrata) del terzo ordine è uguale
alla somma dei prodotti degli elementi della prima
riga per i rispettivi complementi
algebrici:
|
|

|
|
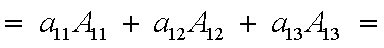
|
|
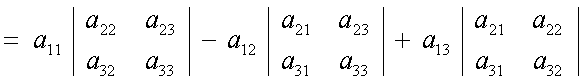
|
Per una matrice di ordine n il determinante è uguale alla somma dei
prodotti degli elementi della prima riga per i rispettivi complementi
algebrici:
|
|

|
|
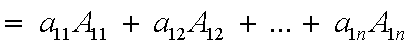
|
Più in generale il determinante di una matrice di ordine n può
essere calcolato secondo la formula:
|
|
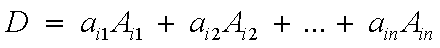
|
dove Ai1 è il complemento algebrico dell'elemento ai1
della i-esima riga. Con tale formula il calcolo del determinante di una matrice
di ordine n può essere ridotto al calcolo di determinanti di matrice di ordine
n-1.
|