Reti neurali e previsioni del tempo
(ultimo aggiornamento:02/10/10
)
Questa pagina proporrà al lettore le nozioni di base sulle
reti neurali e la loro possibile applicazione nel campo delle previsioni locali
del tempo.
I modelli basati sulle reti neurali trovano impiego nei
processi di previsione, di decisione o di classificazione quando la
parametrizzazione matematica risulta irrimediabilmente complessa, introducendo
non-linearità. Essi simulano il tipico modo analogico di pensare degli esseri viventi. A differenza di altri modelli,
quelli a reti neurali possono
essere provati anche sul computer di casa, offrendoci l'opportunità di
sperimentarne il suo funzionamento dal vivo. Utilizzeremo pertanto uno o più programmi
largamente diffusi per condurre i nostri personali esperimenti casalinghi. A tal
proposito, leggi la mia
proposta intorno al gruppo di lavoro sulle reti neurali.
Prima di iniziare il nostro viaggio, cerchiamo di capire a
grandi linee cosa
sono le reti neurali (neural networks).
Una rete neurale simula in maniera elementare alcune funzioni
del cervello umano replicandone la struttura di base, ove ogni singolo neurone è collegato
agli altri mediante
una connessione semplice terminante in una sinapsi. Attraverso questa struttura di base, il cervello umano
è in grado di cogliere relazioni tra oggetti anche se queste non appartengono
alla sua esperienza diretta, basandosi sulle conoscenze già apprese. In altre parole, è in grado di immaginarsi
soluzioni nuove eppure coerenti con la sua base di dati.
Alle reti neurali si chiede di fare altrettanto (con le dovute
limitazioni, s'intende), ovvero di
predire un risultato estrapolandolo per analogia, in maniera non lineare ma coerente, da
quello che ha già imparato. Per ottenere questo risultato, si sottopone la rete
ad un preventivo apprendimento attraverso opportuni esempi, in modo che essa
possa formarsi la sua "esperienza".
Un piccolo esempio ci darà una mano a capire meglio cosa ci si
aspetta dalle reti neurali: un esperto botanico esamina una foglia e individua a
quale specie essa appartiene. Attenzione: egli non ha mai visto quella specifica
foglia, ma usando la sua perizia, ha saputo riconoscerne le caratteristiche
salienti pervenendo alla corretta classificazione della foglia.
Una rete neurale ben addestrata potrebbe essere in grado,
sostanzialmente, di fare la stessa cosa. Tutto ciò di cui essa ha bisogno è di
imparare attraverso esempi corretti, in modo da costruirsi delle ragionevoli
raffigurazioni (pattern) della realtà. In altre parole, se insegno ad
una rete a distinguere un cerchio da un quadrato, essa sarà in grado di farlo a
prescindere dalla dimensione o dal colore delle figure geometriche, perchè si
sarà fatta un'idea di "cerchiosità" e "quadratosità"
(perdonatemi i neologismi!).
Va bene, direte, ma cosa c'entra tutto questo con la
meteorologia?
L'osservazione del tempo è una costante dell'umanità. Il
marinaio, il contadino, il pastore, osservando quotidianamente le condizioni
atmosferiche del suo luogo, affinava una sorta di sensibilità verso le
manifestazioni meteorologiche più evidenti, riuscendo a cogliere relazioni tra
i fenomeni. Numerosissimi sono motti e proverbi "prognostici"
tramandati dalla cultura popolare.
Bene. La rete neurale può fare altrettanto e farlo
scientificamente, individuando, se ve ne sono, relazioni tra parametri osservati
localmente. Volete un esempio: se una tal montagna s'incappuccia di nubi ecc.,
seguiranno precipitazioni e amenità varie. Addestrate la vostra rete con i dati
osservati al momento dell'incappucciamento e insegnategli quando effettivamente
piove o no. Rispetto al contadino, potrete valutare le effettive connessioni
basandovi su un maggior numero di dati scientificamente osservati (temperatura,
rugiada, direzione e intensità del vento, indici di stabilità, ecc.).
Cosa volete di più? Tradizione e scienza intimamente legati in
un sol colpo!
Impariamo un po' di termini specifici
Per impadronirsi di una
disciplina bisogna innanzitutto conoscerne i termini specifici (almeno i più
comuni). E' noto infatti che, specialmente nella letteratura scientifica, molti
termini e concetti sono ritenuti scontati (anche quando non lo sono), rendendo
talvolta difficilmente comprensibile il testo a chi ci si avvicina per imparare (a
volte ho l'impressione che ci sia del dolo prossimo al sadismo in tutto ciò).
Se questo è scusabile in tale tipo di comunicazione umana, è invece
assolutamente imperdonabile nei testi scolastici 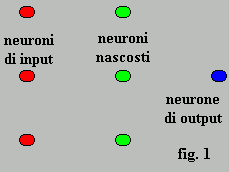 o didattici in genere, che
hanno il dovere di comunicare (ovvero condividere) un sapere (un consiglio a chi
scrive testi didattici di matematica o fisica: scrivete tutti i passaggi!). o didattici in genere, che
hanno il dovere di comunicare (ovvero condividere) un sapere (un consiglio a chi
scrive testi didattici di matematica o fisica: scrivete tutti i passaggi!).
Esistono diversi modelli per reti neurali. I tipi più
importanti sono:
-
Multilayer Perceptrons (reti feedforward)
-
Radial Basis Functions
-
Kohonen (Kohonen Self-Organizing Feature Maps)
-
Reti Neurali Probabilistiche (PNN)
-
Reti Neurali di Regressione Generalizzata (GRNN)
-
Reti Lineari.
Una rete neurale classica (neural network) è composta di neuroni
(figura 1) e di connessioni (figura 2). I neuroni a seconda della funzione svolta si
suddividono in:
-
neuroni di input, input neurons, (cerchietti rossi in fig.1);
rappresentano l'unica porta d'ingresso dei dati forniti dall'esterno.
-
neuroni intermedi o nascosti , hidden neurons,(cerchietti verdi in
fig.1);
-
neuroni di output, output neurons, (cerchietti blu in fig.1).
 Le connessioni impropriamente definite sinapsi
(synapses) costituiscono gli elementi fondamentali di una rete, e
consentono di interconnettere un neurone con i neuroni dello strato successivo.
Le connessioni possiedono le seguenti caratteristiche: Le connessioni impropriamente definite sinapsi
(synapses) costituiscono gli elementi fondamentali di una rete, e
consentono di interconnettere un neurone con i neuroni dello strato successivo.
Le connessioni possiedono le seguenti caratteristiche:
-
partono da un neurone;
-
giungono ad altro neurone;
possiedono un "peso" (weight).
Generalmente una buona sinapsi avrà un peso maggiore rispetto ad una
cattiva sinapsi.
Le reti, regolate da algoritmi,
imparano attraverso due parametri fondamentali, ovvero:
-
la funzione di attivazione dei neuroni;
-
la regola di apprendimento della rete.
La funzione di
attivazione dei neuroni entra in gioco quando nel neurone giungono in
ingresso i valori (gli input) provenienti dal precedente strato neuronale.
Questa funzione può essere a gradino o continua differenziabile detta "sigmoide".
In breve, quando nel neurone giungono i segnali provenienti dai neuroni dello
strato precedente, esso li trasforma attraverso una funzione, che determina il
segnale da inviare al neurone dello strato successivo.
La regola si
apprendimento consente l'introduzione di conoscenze nella rete, mediante
una serie opportuna di esempi.
Gli algoritmi consentono l'auto-modifica iterativa dei pesi
delle connessioni tra i neuroni. In parole povere, la rete imparerà dai propri
errori.
Per capire cosa significa, immaginatevi mentre
state lanciando una pietra per colpire un oggetto in movimento: all'inizio non
saprete quanta forza occorrerà. Il vostro apprendimento comincia col lanciare
la pietra e valutandone gli effetti. Se il lancio è troppo lungo o troppo
corto, al tiro successivo correggerete traiettoria e forza, e questo finché il
vostro obiettivo non sarà raggiunto: state modificando dinamicamente i dati di
base. Se il vostro obiettivo si muoverà, sarete in grado di colpirlo anche se
la posizione che occupa sarà nuova, e questo proprio perché l'addestramento
effettuato vi consentirà di valutare quanta forza e quale traiettoria più o
meno dovrete applicare.
E' in tal modo che la rete acquista l'abilità di
generalizzare la funzione appresa: infatti, assegnandole un valore non compreso
tra gli esempi, essa sarà in grado comunque di fornire un responso basandosi su
quanto ha imparato, ovvero saprà valutare in maniera non lineare quanta
influenza ("peso") ha ciascuna connessione nel produrre un dato di
output. In altre parole essa saprà dare il giusto peso ad ogni elemento,
producendo la risposta più "assennata" (se così si può dire!).
Affinché non rimaniate a bocca aperta se qualcuno vi
"spara" paroloni (magari in inglese), accennerò brevemente ad alcuni
degli algoritmi maggiormente utilizzati:
On-line Back
Propagation (noto anche come Stochastic Back Propagation) o più
semplicemente "metodo della propagazione all'indietro o retropropagazione
dell'errore"; in
genere viene considerato il più veloce metodo di apprendimento. In questo
algoritmo i pesi delle connessioni vengono aggiornati dopo ogni ciclo di
addestramento, cioè, eseguito il primo ciclo, la rete valuterà di quanto ha
sbagliato e modificherà i pesi delle connessione in modo da minimizzare
l'errore, e così via per tutti i restanti cicli. E' uno dei due algoritmi utilizzati nel programma Neural Planner.
Batch Back Propagation;
è una variante dell' On-line Back Propagation. Con questo algoritmo i pesi vengono
cumulati e corretti alla fine.
Extended Back
Propagation for Sequences (EBPS) dell'errore: è una regola di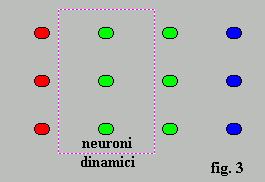 apprendimento che consente di
simulare una sorta di memoria della rete mediante un feedback posto sullo
strato di neuroni nascosti (hidden neurons layer) immediatamente
successivo allo strato di input. Per tale motivo questi neuroni vengono definiti
"dinamici" (fig.3). I
neuroni appartenenti al successivo strato di neuroni nascosti saranno per contro
definiti "neuroni statici". apprendimento che consente di
simulare una sorta di memoria della rete mediante un feedback posto sullo
strato di neuroni nascosti (hidden neurons layer) immediatamente
successivo allo strato di input. Per tale motivo questi neuroni vengono definiti
"dinamici" (fig.3). I
neuroni appartenenti al successivo strato di neuroni nascosti saranno per contro
definiti "neuroni statici".
A chiusura di queste brevi note, occorre dire che la ricerca
topologica ottimale (in genere effettuata attraverso un processo
"prove ed errori") richiede numerosi esperimenti. Fatto ciò, si
procederà nella taratura della
rete stessa e nella valutazione della
sua affidabilità.
Se ti va di partecipare al nostro viaggio nelle reti neurali,
procedi con il download del
programma (Neural Planner). E' un file in formato .zip di circa 648 Kb. Una
volta installato, comincia con la prima lezione,
in cui ti spiego come disegnare la rete. Prosegui poi con la seconda
lezione, in cui imparerai ad attribuire ad ogni neurone il suo nome. Le
successive lezioni (in corso di preparazione), illustreranno come inserire gli
esempi e far "girare" la rete. Appresi i concetti principali, nella
sezione Applicazioni, potrai trovare esempi attraverso cui imparare ad applicare
le reti neurali alla meteorologia.
Buon viaggio!
Bibliografia. in
italiano:
PASINI, A., PELINO, V., POTESTA', S., - Un modello reticolare
di neuroni artificiali per la previsione della visibilità meteorologica. Parte
prima: gli aspetti teorici, Riv.Met.Aer., vol.58, nn.1-2, Roma, 1998 RICH,
E., KNIGHT, - Intelligenza artificiale, McGraw Hill. ROLSTON,
D.W., - Sistemi esperti, McGraw Hill. RONCHINI,
G., SALVEMINI, C.M., VECCIA, E., - Previsioni locali automatiche: approccio
mediante reti neurali, Riv.Met.Aer., vol.56, nn.1-2, Roma, 1996. SALVEMINI,
C.M., - Approccio neuronale alla previsione meteorologica, Tesi di
laurea, Università di Milano, 1990. in inglese:
ANDERSON, J.A., ROSENFELD, E., - Neurocomputing: Foundations
of Research, MIT Press, Cambridge MA., 1988. FAUSSET, L.V.,
- Fundamentals of Neural Networks: Architectures, Algorithms, and
Applications, Prentice Hall. (Clicca qui per una
breve descrizione del libro).
GORI, M., BENGIO, Y., DE MORI, R., - A learning algorithm for
capturing the dynamic nature of speech, Proc. of the IEEE-IJCNN, Washington,
1989. MINSKY M., PAPERT, S., - Perceptrons, MIT Press,
Cambridge MA, 1988. PASINI, A., PELINO, V., POTESTA', S. - A
neural network model for visibility nowcasting from surface observation: Results
and sensitivity to physical input variables, Journal of Geophysical Research,
vol.106, n. D14, 2001 (Abstract). PASINI, A., POTESTA', S., Short-range
visibility forecast by means of neural-network modelling, Nuovo Cimento,
18C, 1995. PASINI, A., POTESTA',S., Neural network modelling:
Perspectives of application for monitoring and forecasting physical-chemical
variables in the boundary layer, in Urban Air Pollution, edito da
I.Allegrini e F.De Santis, Springer-Verlag, New York, 1996 PASINI,
A., POTESTA',S., Towards fog forecasting in meteorology by means of
back-propagation neural networks with weighted least-squares training,
in Neural Nets: WIRN Vietri-96, edito da M.Marinaro e R.Tagliaferri,
Springer-Verlag, New York, 1997. RUMELHART, D.E., McCLELLAND, J.L., - Parallel
Distributed Processing: Explorations in the Microstructure of
Cognition , The MIT Press, 1986. WASSERMAN, P., - Neural computing
theory and practice, Van Nostrand, New York, 1989.
Link di grande interesse:
(Rev.02/2001)
|