Trigonometria sferica
(Ultimo aggiornamento:02/10/10
)
VETTORE,NOTAZIONE DI GRASSMAN, VETTORI EQUIMODULO, VETTORI PARALLELI,
VETTORI CONCORDI, VETTORI DISCORDI, VETTORI OPPOSTI, VERSORE, VERSORI
FONDAMENTALI DI RIFERIMENTO, SFERA TRIGONOMETRICA, ROTAZIONE VETTORIALE o
PERMUTAZIONE CICLICA, CERCHIO MASSIMO FONDAMENTALE, POLO ELEVATO DEL
CERCHIO MASSIMO FONDAMENTALE, TRIANGOLO SFERICO EULERIANO, ANGOLI DIEDRI
DEL TRIEDRO, TRIANGOLO SFERICO RETTANGOLO, TRIANGOLO SFERICO RETTILATERO,
TRIEDRO, TRIANGOLO SFERICO POLARE, VETTORE RISULTANTE, REGOLA DEL
PARALLELOGRAMMA,EQUAZIONE VETTORIALE DEL CERCHIO MASSIMO DELLA SFERA
TRIGONOMETRICA, PROIEZIONE POLARE DI UN PUNTO R, COORDINATE POLARI DEL
PUNTO R, ASCISSA POLARE SFERICA, ORDINATA SFERICA POLARE,TRIRETTANGOLO
FONDAMENTALE, TEOREMA DI EULERO, TEOREMA DELLE PROIEZIONI, TEOREMA DEI
SENI, FORMULE FONDAMENTALI DELLA TRIGONOMETRIA SFERICA o PRIMA TERNA DI
GAUSS o PRIMO GRUPPO SFERICO, FORMULE CORRELATIVE DELLE FONDAMENTALI o
SECONDA TERNA DI GAUSS o SECONDO GRUPPO SFERICO, FORMULE DEL VIETA,
TEOREMA DELLE COTANGENTI, RELAZIONE DEL CAGNOLI, ECCESSO SFERICO e,
FORMULE DI BORDA, FORMULE DI DELAMBRE, FORMULE DI NEPERO o ANALOGIE DI
NEPERO, TRIANGOLO SFERICO RETTANGOLO, IPOTENUSA, CATETI, REGOLA MNEMONICA
DI NEPERO, TRIANGOLO SFERICO RETTILATERO, PROBLEMA FONDAMENTALE DELLA
TRIGONOMETRIA SFERICA, SISTEMI DI MISURE ANGOLARI, SISTEMA SESSAGESIMALE,
SISTEMA CENTESIMALE, SISTEMA SESSADECIMALE, SISTEMA MILLESIMALE
CONVENZIONALE, SISTEMA ORARIO, SISTEMA ANALITICO,RADIANTE
|
|
|
(pag.18) Ente fisico-matematico che possiede contemporaneamente le seguenti
proprietà: modulo, direzione, verso.
|
NOTAZIONE DI GRASSMAN
|
(pag.18)
|
|
|
(pag.19) Due vettori aventi lo stesso modulo.
|
|
|
(pag.19) Due vettori aventi la stessa direzione.
|
|
|
(pag.19) Vettori aventi lo stesso verso.
|
|
|
(pag.19) Vettori che non hanno lo stesso verso.
|
|
|
(pag.19) Vettori equimoduli, paralleli e discordi.
|
|
|
(pag.19) Quel vettore avente modulo uguale all'unità di misura assunta.
|
|
|
(pag.20)
|
|
|
(pag.21) Superficie appartenente ad una sfera di raggio unitario
individuata dagli infiniti versori uscenti dal punto O.
|
|
|
(pag.22)
|
|
|
(pag.23)
|
|
|
(pag.23)
|
TRIANGOLO SFERICO EULERIANO
|
(Anche TRIANGOLO SFERICO ORDINARIO, pag.23). Porzione di superficie sferica
limitata, sulla sfera trigonometrica, da tre archi di cerchio massimo di
misura inferiore a 180°, che s'incontrano fra loro in tre punti detti
vertici.
|
ANGOLI DIEDRI DEL TRIEDRO
|
(pag.24) Angoli ai vertici del triangolo sferico.
|
|
|
(pag.25) Se uno dei suoi angoli è retto.
|
|
|
(pag.25) Se uno dei suoi lati misura 90°.
|
TRIEDRO
|
|
TRIANGOLO SFERICO POLARE
|
|
VETTORE RISULTANTE
|
|
REGOLA DEL PARALLELOGRAMMA
|
|
EQUAZIONE VETTORIALE DEL CERCHIO MASSIMO DELLA SFERA TRIGONOMETRICA
|
|
PROIEZIONE POLARE DI UN PUNTO R
|
(pag.36) Dato un qualsiasi punto R della superficie sferica, è
l'arco di cerchio massimo condotto dal volo P, passante per R, e compreso
fra il polo elevato ed il suo cerchio massimo.
|
COORDINATE POLARI DEL PUNTO R
|
-
Ascissa polare sferica
Ordinata sferica polare o distanza polare
|
ASCISSA POLARE SFERICA
|
|
ORDINATA SFERICA POLARE
|
|
TRIRETTANGOLO FONDAMENTALE
|
(pag.37)
|
|
|
(pag.41) Una delle tre formule fondamentali della trigonometria
sferica. In un triangolo sferico ordinario il coseno di un lato (cos
a) è uguale al prodotto dei coseni degli altri due (cos b cos c), più il
prodotto dei loro seni moltiplicato per il coseno dell'angolo fra essi
compreso (sen b sen c cos A).
Cos a = Cos b Cos c + Sin b Sin c
Cos A
Cos b = Cos a Cos c + Sin a Sin c Cos B
Cos c = Cos a Cos b + Sin a Sin b Cos B
|
|
|
(pag.42) Una delle tre formule fondamentali della trigonometria
sferica. In un triangolo sferico ordinario il prodotto del seno di
un lato per il coseno di uno degli angoli adiacenti (sen a cos C) è
uguale al prodotto del coseno del lato opposto all'angolo considerato per
il seno del rimanente lato (cos c sen b), meno il prodotto del seno del
lato opposto all'angolo considerato inizialmente per il coseno del
rimanente lato moltiplicato per il coseno dell'angolo opposto al primo
lato considerato (sen c cos b cos A).
Si ottengono così sei relazioni fra cinque elementi: tre lati e due
angoli.
|
|
|
(pag.43) Una delle tre formule fondamentali della trigonometria
sferica. In ogni triangolo sferico ordinario i seni dei lati sono
proporzionali ai seni degli angoli opposti.
Sin A
-------
Sin a
|
=
|
Sin B
-------
Sin b
|
=
|
Sin C
-------
Sin c
|
|
FORMULE FONDAMENTALI DELLA TRIGONOMETRIA SFERICA o PRIMA TERNA DI
GAUSS o PRIMO GRUPPO SFERICO
|
(pag.40, 43) Sono dette fondamentali perché, combinandole
opportunamente, si possono dedurre attraverso semplici passaggi
matematici, tutte le altre.
|
|
|
(pag.46) Data una qualsiasi relazione di trigonometria sferica,
formule che si ottengono sostituendo semplicemente, al posto dei lati che
vi figurano:
a= 180° - A; b = 180° -B; c = 180° - C
ed agli angoli A,B, C che in essa figurano sostituendo:
A= 180° - a; B = 180° - b; C = 180°- c.
|
|
|
(pag.48)
|
|
|
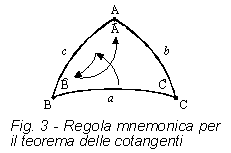 (pag.48) Il prodotto
della cotangente di un lato per il seno di uno degli altri due lati è
uguale al prodotto del coseno del lato scelto per il coseno dell'angolo
fra essi compreso più il prodotto del seno di quest'angolo per la
cotangente dell'angolo opposto al lato scelto come iniziale.
|
|
|
(pag.49)
|
|
|
(pag.51) E' la differenza e = (A + B + C)
- 180°.
|
|
|
(pag.52)
|
|
|
(pag.57)
|
|
|
(pag.60) Relazioni molto importanti perché di uso frequente nella
risoluzione dei triangoli sferici astronomici, cioè di quei particolari
triangoli sferici che vengono usati nei lavori d'ingegneria e nella
navigazione.
|
TRIANGOLO SFERICO RETTANGOLO
|
(pag.62) Un triangolo sferico si dice rettangolo quando uno dei suoi
angoli è uguale ad un angolo retto.
|
|
|
(pag.62)
|
|
|
(pag.62)
|
|
|
 (pag.65) Regola per
ricordare facilmente le dieci formule relative al triangolo sferico
rettangolo. In un triangolo sferico rettangolo, se si prescinde
dall'angolo retto e se ai cateti si sostituiscono i loro complementi, il
coseno di uno qualunque dei cinque elementi restanti è uguale al prodotto
delle cotangenti dei due elementi adiacenti e al prodotto dei seni dei due
elementi opposti.
|
TRIANGOLO SFERICO RETTILATERO
|
(pag.71) Un triangolo sferico si dice rettilatero quando uno dei suoi
lati è uguale a 90°.
|
PROBLEMA FONDAMENTALE DELLA TRIGONOMETRIA SFERICA
|
(pag.72) Consiste nel trovare, quando sia possibile, tre degli
elementi di un triangolo sferico, conoscendo gli altri tre,
|
SISTEMI DI MISURE ANGOLARI
|
(pag.111) Si possono distinguere in geometrici e analitici. Sono
geometrici quelli in cui l'unità di misura è sottomultiplo dell'angolo
retto.
|
SISTEMA SESSAGESIMALE
|
(pag.111)
|
SISTEMA CENTESIMALE
|
(pag.112)
|
SISTEMA SESSADECIMALE
|
(pag.112)
|
SISTEMA MILLESIMALE CONVENZIONALE
|
(pag.113)
|
SISTEMA ORARIO
|
(pag.113)
|
SISTEMA ANALITICO
|
(pag.113)
|
RADIANTE
|
(pag.113)
|
|
