(1) Quale forza costante si deve applicare al corpo di 10 kg per
fargli acquistare in 5s la velocità di 40 m/s?
|
(dati) m = 10kg, t = 5s, v = 40 m/s
|
(incognite) F?
|
|
(2) Un corpo di massa di 2kg
subisce una forza verso l'alto di (a) 6N (b) 8000 dine. Calcolare
l'accelerazione in ciascun caso.
|
Da
|
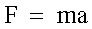
|
ricaviamo l'accelerazione
|
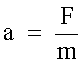
|
(a)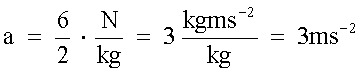
|
(b) Poiché nel sistema CGS,
l'unità di massa è il grammo, 2 kg = 2000 g
|
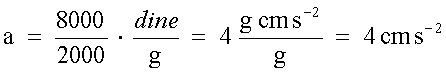
|
(3) Trovare la forza richiesta per imprimere ad un blocco del peso di
6 kg l'accelerazione di 3 m/s-2.
|
(dati) w=6kg, a=3m/s-2
|
(inc) Forza F?
|
Per poter applicare la seconda legge della dinamica F=ma,
dobbiamo conoscere il valore della massa. Sappiamo che il peso w=mg,
da cui possiamo facilmente ricavare la massa m:
|
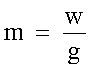
|
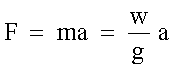
|
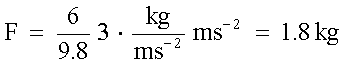
|
(4) Una locomotiva del peso di 10 t spinge un treno del peso di 50 t
lungo un binario orizzontale imprimendogli un'accelerazione a1=1ms-2.
Quale accelerazione a2 imprimerebbe il locomotore ad un treno
del peso di 20 t esercitando la stessa forza?
|
(dati) w1=10t=10000kg, w2=50t=50000kg, w3=20t=20000kg,
a1=1ms-2
|
(inc) a2=?
|
Partendo dalla seconda legge della dinamica, dobbiamo trovare la massa
su cui si esercita la forza F per imprimere l'accelerazione di 1ms-2.
|
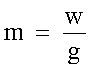
|
Per il sistema locomotiva + treno dal peso w2, il peso
complessivo è dato da w1+w2, quindi la massa totale
m1 sarà data da
|
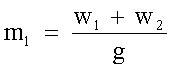
|
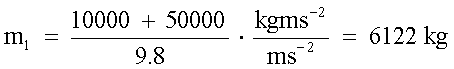
|
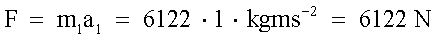
|
Per il sistema locomotiva + treno dal peso w3, il peso
complessivo è dato da w1+w3, quindi la massa totale
m2 sarà data da
|
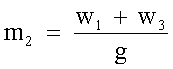
|
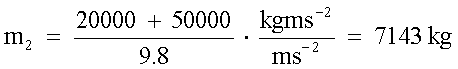
|
dalla F=m2a2
ricaviamo l'accelerazione a2:
|
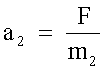 |
|
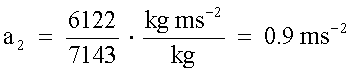
|
(5) Un'automobile del peso di 1000 kg viaggia alla velocità di 90
km/h. Calcolare la forza rallentante dei freni necessaria per fermarla in
70 m su di un percorso orizzontale.
|
(dati) w=1000kg, v=90km/h, s=70m
|
(inc) Forza f?
|
| |
|