(A1) Qual è il peso (in N) di un uomo di 80 kg (di massa)?
|
(dati) m = 80 kg
|
(inc) w = ?
|
Risoluzione:
Sappiamo che il peso w = mg
g = 9.8 m s-2
w=80 * 9.8 * kg m s-2 = 784 kg m s-2
Poiché 1 newton è = 1kg * 1 m s-2, 784 kg m
s-2 = 784 N
|
(A2) Qual è il peso (in N) di un uomo di 80 kg (di massa) sulla Luna
sapendo che g vale 1.6 m s-2 ?
|
(dati) m = 80 kg
|
(inc) w = ?
|
Risoluzione:
Sappiamo che il peso w = mg
g = 1.6 m s-2
w = 80 * 1.6 * kg m s-2 = 128 kg m
s-2
Poiché 1 newton è = 1kg * 1 m s-2 allora 128
kg m s-2 = 128 N
|
(A3) Qual è il peso (in N) di un uomo di 80 kg (di massa) su Giove
sapendo che g vale 24 m s-2 ?
|
(dati) m = 80 kg
|
(inc) w = ?
|
Risoluzione:
Sappiamo che il peso w = mg
g = 24 m s-2
w = 80 * 24 * kg m s-2 = 1920 kg m
s-2
Poiché 1 newton è = 1 kg * 1 m s-2 allora
1920 kg m s-2 = 1920 N.
|
(A4) Calcolare il peso w di un corpo la cui massa è (a) 1 kg (b) 1g.
|
(dati) m1 = 1kg, m2 = 1g
|
(inc) peso w?
|
Giova qui ricordare che il peso di un corpo è la forza dovuta alla
gravità, la cui direzione si trova sulla retta che passa
approssimativamente per il centro della Terra.
|
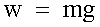
|
(a)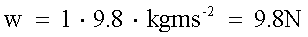
|
(b) 1g = 0.001 kg
|
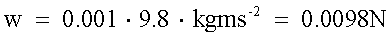
|
(5) Trovare la massa m di un corpo il cui peso w è (a) 19,6N (b) 1960
dine.
|
(a) Ricordando che nel sistema MKS l'unità di forza è il newton (N),
la legge
|
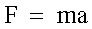
|
si esprime dimensionalmente come
|
1N = 1kg * 1ms-2
(non si dimentichi che nel sistema MKS il kg è l'unità fondamentale di
massa).
|
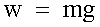
|
da cui ricaviamo
|
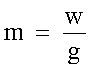
|

|
(b) Ricordando che nel sistema CGS l'unità derivata di forza è la
dina, la legge
|
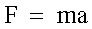
|
si esprime dimensionalmente come
|
1dina = 1g * 1cms-2
(non si dimentichi che nel sistema CGS il grammo g è l'unità
fondamentale di massa, mentre l'accelerazione è espressa in cms-2).
|
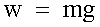
|
da cui ricaviamo
|
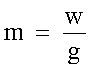
|
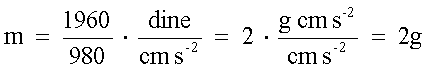
|